The Magic Behind Clear Images: Sampling Theory and Aliasing

Have you ever wondered how a camera captures images without missing important details or introducing unwanted artifacts? The answer lies in the concept of sampling theory. In this article, we will explore the fascinating world of sampling theory and the phenomenon of aliasing in image processing.

From Continuity to Discreteness: Capturing the Image

When we take a photo, the lens of the camera forms a continuous optical image on the image plane. However, to convert this continuous image into a digital image, it needs to be sampled. The question is, how densely should we sample the continuous image to ensure we don’t lose crucial information while avoiding any undesirable effects in the final captured image?

The Essence of Sampling Theory

Sampling theory provides us with the guidelines for sampling the continuous image. Let’s imagine we have a continuous image formed on the image plane. To obtain a discrete signal, we sample this continuous image. The crucial question now is, how densely should we sample the continuous image? What should be the distance between consecutive samples?

The Problem of Aliasing

To understand the problem of aliasing, let’s consider a simple example. Imagine we have a sinusoidal signal and its higher-frequency version. If we sample both of these signals with the same frequency, we may end up with a reconstructed signal that closely resembles the original. However, if the sampling is inadequate, we may experience aliasing, where important information is lost and artifacts are introduced into the image.

The Visual Manifestation of Aliasing

Aliasing becomes visually apparent when we under-sample an image. For example, a well-sampled image of a brick wall with high-frequency texture looks fine. However, when we under-sample the image, we observe patterns, waves, and ripple effects known as moiré patterns, which are unwanted artifacts caused by aliasing.

The Theory of Sampling: Delving into the Mathematics

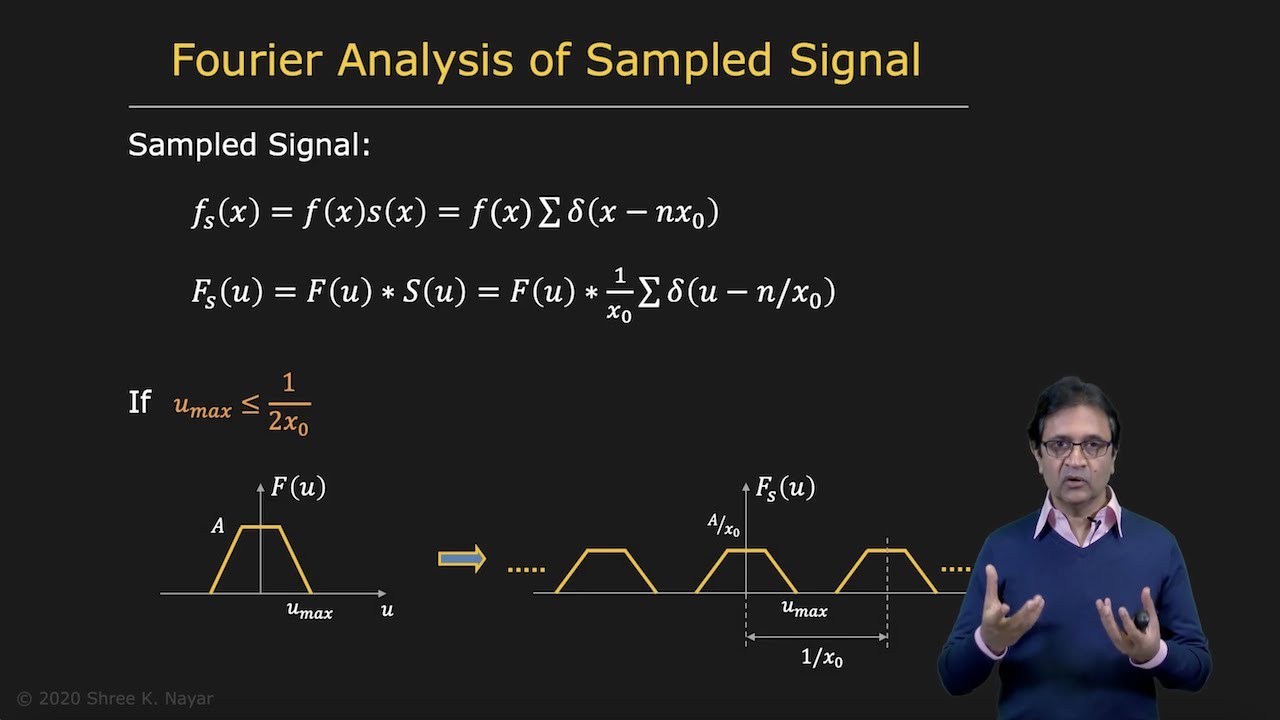
To develop a theory of sampling, we start with a continuous signal. This continuous signal is sampled by multiplying it with an impulse train, also known as the shah function. The shah function consists of delta functions displaced by a specific distance. The resulting sampled function, denoted as fs, is obtained by multiplying the continuous signal with the shah function.

The Fourier Transform: Understanding Frequency Domain

To understand the effect of sampling in the frequency domain, we examine the Fourier transform of the sampled signal. The Fourier transform of the shah function is another shah function, but with a different period. By convolving the Fourier transform of the continuous signal with the shah function, we obtain multiple copies of the original signal, spaced apart by a particular frequency.

Overlapping Copies and the Problem of Aliasing

When the maximum frequency in the continuous signal, denoted as u max, is less than or equal to half the distance between the copies, aliasing is avoided. However, if u max exceeds this threshold, the copies overlap, leading to the introduction of new frequencies and artifacts in the image.

Nyquist Theorem: A Solution to Aliasing

The Nyquist theorem guides us in determining whether an image is well-sampled or under-sampled. If the maximum frequency in the image is less than or equal to half the sampling frequency, the image is well-sampled. However, if the maximum frequency exceeds this threshold, aliasing occurs, and artifacts are present in the image.

Devising Strategies to Minimize Aliasing

Although we have no control over the frequencies that arrive at the camera lens, we can minimize the effects of aliasing by designing the image sensor and using optical filters. The pixels on the image sensor collect light falling on a finite area, effectively low-pass filtering the image. Additionally, an optical filter can be used to cut out frequencies above the Nyquist frequency, ensuring that the captured image is free from aliasing.

In conclusion, sampling theory and understanding aliasing are crucial in ensuring clear and artifact-free images. By adhering to the principles of sampling theory and employing appropriate techniques, we can capture images with precision and accuracy. Next time you snap a photo, remember the magic behind it: sampling theory and the avoidance of aliasing.

For more exciting articles about the fascinating world of information technology, visit Techal.