Have you ever wondered how a periodic function can be represented as a sum of sinusoids? Well, that’s where the incredible Fourier transform comes into play. Named after Joseph Fourier, this mathematical concept has had a profound impact on various scientific and engineering disciplines.
Contents
The Journey of the Fourier Transform
Joseph Fourier was a mathematician who was fascinated with heat propagation through different shapes of materials. His curiosity and obsession with the topic led him to develop the Fourier transform. This transformative concept states that any periodic function can be expressed as a weighted sum of infinite sinusoids with different frequencies.
Imagine that – any function can be written as a sum of sinusoids! This groundbreaking idea has revolutionized the field of science and engineering. In fact, it would be hard to imagine the technological advancements of the past 50 years without the existence of the Fourier transform.
Understanding Sinusoids
Before diving deeper into the Fourier transform, let’s familiarize ourselves with sinusoids. A sinusoid is a mathematical function that represents a wave-like pattern. It is characterized by its amplitude, frequency, period, and phase.
Unveiling the Fourier Transform
So what exactly does the Fourier transform do? It represents a function in terms of the amplitudes and phases of its constituent sinusoids. By applying the Fourier transform to a signal in the spatial domain, we can express it in the frequency domain. This transformation allows us to understand the different frequencies present in the signal and their corresponding amplitudes and phases.
The Fourier transform and its inverse counterpart are represented by integrals. The Fourier transform takes a signal in the spatial domain, denoted as f(x), and transforms it into the frequency domain, denoted as F(u). The inverse Fourier transform does the opposite, converting the frequency representation back to the spatial representation.
It’s important to note that neither the Fourier transform nor the inverse Fourier transform result in a loss of information. The two representations are equivalent and can be seamlessly switched between without any loss.
Complex Nature of the Fourier Transform
The Fourier transform involves complex numbers to fully capture the amplitude and phase of each sinusoid. These complex numbers hold the key to understanding the frequency content of the signal. The Fourier transform utilizes both positive and negative frequencies, thereby providing a complete representation of the signal.
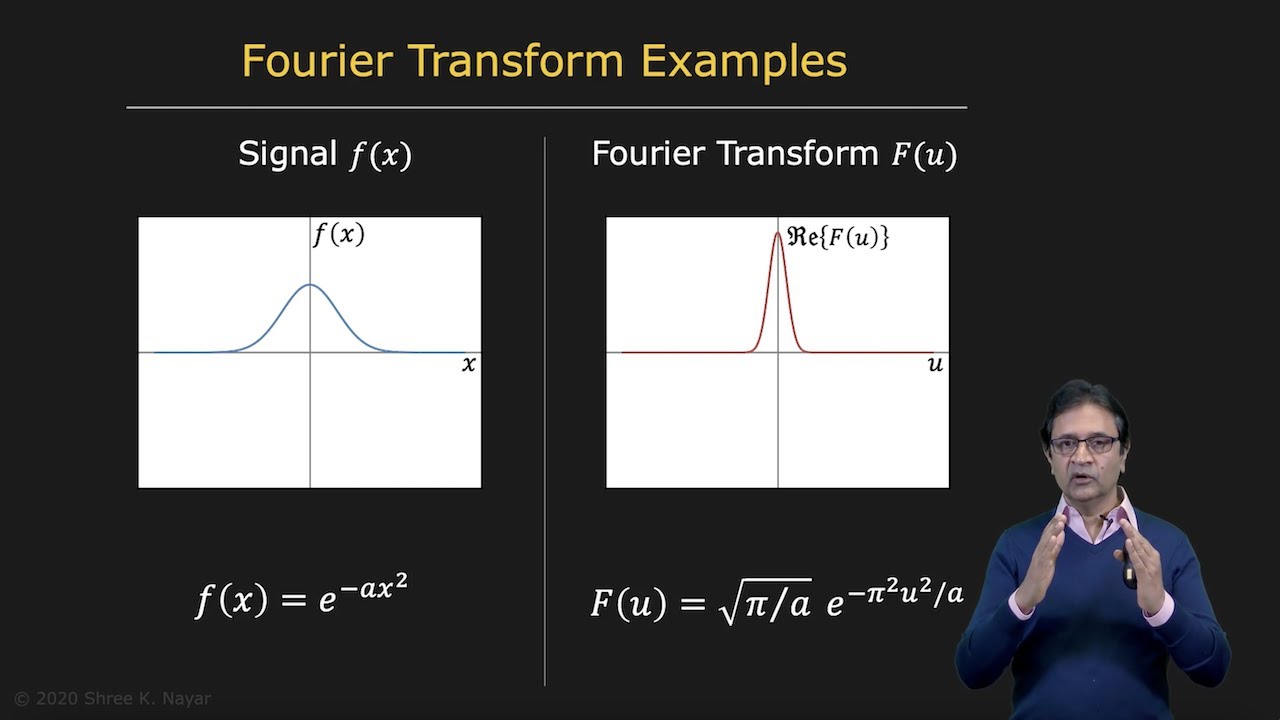
Examples and Properties of the Fourier Transform
To illustrate the power of the Fourier transform, let’s look at some examples. For a cosine function, its Fourier transform is a delta function located at a specific frequency. Two cosine functions with different frequencies result in the sum of their respective Fourier transforms. A sinusoidal function, which is a shifted cosine function, also possesses a delta function in its Fourier transform.
Other examples include a constant signal with a Fourier transform represented by a delta function at 0 and a delta function itself, which requires equal sinusoids of all frequencies to recreate the original signal.
The Fourier transform also exhibits important properties. It is linear, meaning the transform of a linear combination of functions is the same linear combination of their individual Fourier transforms. Scaling a function in the spatial domain leads to an inverse scaling of its Fourier transform in the frequency domain. Shifting a function by a certain amount can be achieved by multiplying its Fourier transform by a complex exponential. Finally, finding the n-th derivative of a function in spatial domain can be done by multiplying its Fourier transform by a power of u.
FAQs
Q: What is the Fourier transform?
A: The Fourier transform is a mathematical concept that represents a function in terms of the amplitudes and phases of its constituent sinusoids. It allows us to express a function in the frequency domain, revealing the different frequencies present in the signal.
Q: Why is the Fourier transform complex?
A: The Fourier transform employs complex numbers to fully capture both the amplitude and phase of each sinusoid. This complex nature is necessary for a mathematically complete representation of the frequency content of the signal.
Q: What are some important properties of the Fourier transform?
A: The Fourier transform is linear, meaning it preserves linearity when applied to a linear combination of functions. It exhibits scaling properties, where scaling a function in the spatial domain results in an inverse scaling of its Fourier transform in the frequency domain. Shifting a function can be achieved by multiplying its Fourier transform by a complex exponential. Additionally, the Fourier transform allows us to easily compute the derivatives of a function in the frequency domain.
Conclusion
The Fourier transform is a remarkable mathematical tool that has revolutionized our understanding of signals and frequency content. It allows us to analyze and manipulate functions by expressing them as a sum of sinusoids. The applications of the Fourier transform are vast and can be found in various scientific and engineering disciplines. Explore the incredible world of the Fourier transform, and unlock new possibilities in your technological endeavors.
Check out Techal for more exciting articles on technology and stay up-to-date with the latest advancements in the field.


