Solving systems of equations is an essential skill in mathematics and can be applied to various real-life scenarios. In this article, we will explore how to solve a 3×3 system of equations with three unknown variables. We will also discuss the concept of the inverse of a matrix and its practical application in solving systems of equations.
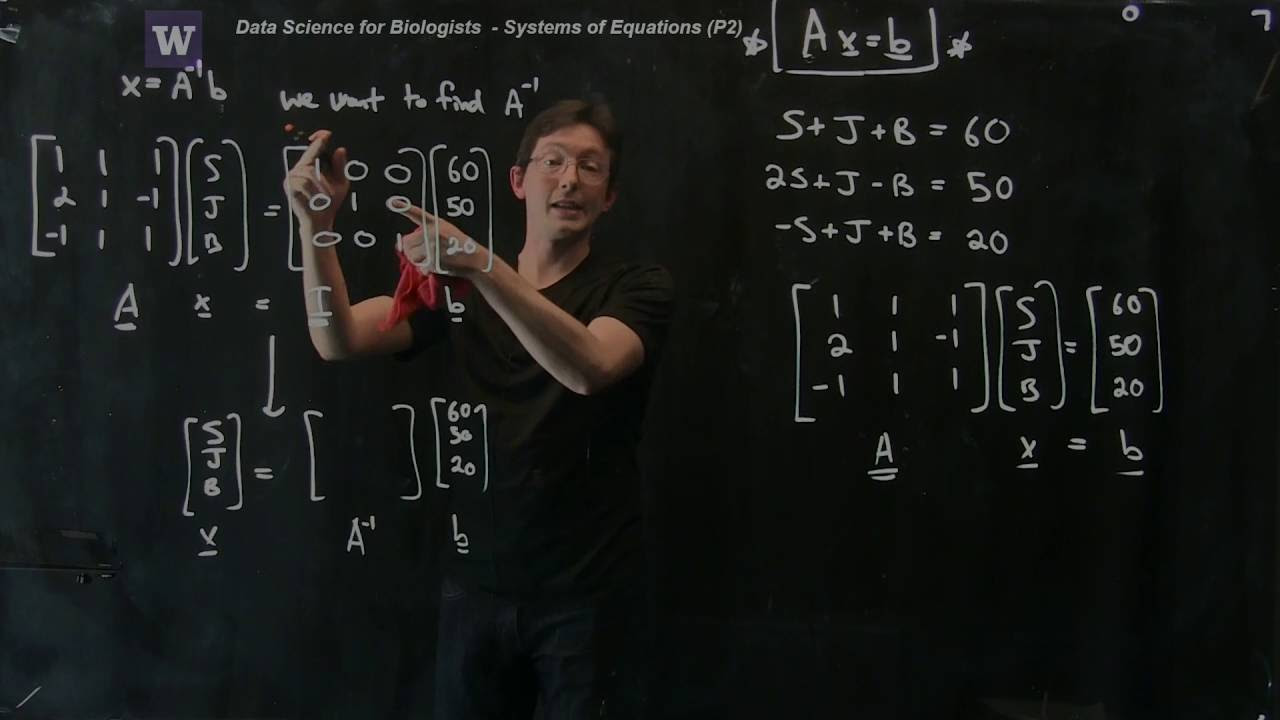
Contents
- Introduction
- The Inverse of a Matrix
- Solving a 3×3 System of Equations
- Applying Operations to Transform the Coefficient Matrix
- Step 1: Subtracting Two Times the First Row
- Step 2: Adding the First Row to the Third Row
- Step 3: Subtracting the Middle Row from the First Row
- Step 4: Adding 2 Times the Middle Row to the Third Row
- Step 5: Subtracting 4 Times the Bottom Row from the Second Row
- Step 6: Subtracting 3 Times the Bottom Row from the First Row
- Final Result: Inverse Matrix
- Solving the System of Equations
- FAQs
- Conclusion
Introduction
Imagine you have a system of equations representing different variables, such as the ages of Sally, John, and Bob. The challenge is to find the values of these variables that satisfy all the given equations.
In addition to solving this system for a specific set of values, what if the values or the equations themselves change? It would be inefficient to repeat the same calculations every time. That’s where the concept of the inverse matrix comes into play.
The Inverse of a Matrix
The inverse of a matrix is a unique matrix that, when multiplied with the original matrix, results in the identity matrix. The identity matrix is a special matrix that, when multiplied with any vector, returns the same vector.
To solve a system of equations repeatedly, we want to find the inverse of the coefficient matrix. By storing the inverse, we can efficiently solve different systems by simply multiplying the inverse with the given vector.
Solving a 3×3 System of Equations
Let’s consider a system of equations with three variables: Sally, John, and Bob.
- Sally + John + Bob = 60
- 2Sally + John – Bob = 50
- -Sally + John + Bob = 20
We can represent this system using a coefficient matrix, denoted as “a”, and a vector of the given values, denoted as “b”. The matrix “a” consists of the coefficients of the variables, while “b” represents the values on the right side of the equations.
Next, we want to transform the coefficient matrix “a” into the identity matrix and perform the same operations on the identity matrix to obtain the inverse matrix. This will allow us to solve the system of equations efficiently.
Applying Operations to Transform the Coefficient Matrix
To transform the coefficient matrix into the identity matrix, we perform a series of operations while keeping track of the transformations.
- Subtract 2 times the first row from the second row.
- Add the first row to the third row.
- Subtract the middle row from the first row.
- Add 2 times the middle row to the third row.
- Subtract 4 times the bottom row from the second row.
- Subtract 3 times the bottom row from the first row.
Note that we apply the same corresponding operations to the identity matrix.
After all the operations, the coefficient matrix should look like the identity matrix, and the identity matrix should become the inverse matrix. Let’s perform these operations step by step.
Step 1: Subtracting Two Times the First Row
We subtract 2 times the first row from the second row and add the first row to the third row. The matrix transformations are as follows:
Step 2: Adding the First Row to the Third Row
We add the first row to the third row. The matrix transformations are as follows:
Step 3: Subtracting the Middle Row from the First Row
We subtract the middle row from the first row and add 2 times the middle row to the third row. The matrix transformations are as follows:
Step 4: Adding 2 Times the Middle Row to the Third Row
We add 2 times the middle row to the third row. The matrix transformations are as follows:
Step 5: Subtracting 4 Times the Bottom Row from the Second Row
We subtract 4 times the bottom row from the second row. The matrix transformations are as follows:
Step 6: Subtracting 3 Times the Bottom Row from the First Row
We subtract 3 times the bottom row from the first row. The matrix transformations are as follows:
Final Result: Inverse Matrix
After the transformations, the coefficient matrix becomes the identity matrix, and the identity matrix becomes the inverse matrix. The final result is as follows:
Solving the System of Equations
To solve the system of equations, we multiply the inverse matrix by the vector “b”.
The solution vector, which represents the ages of Sally, John, and Bob, is as follows:
- Sally = 20
- John = 25
- Bob = 15
By applying this method, we can efficiently solve different systems of equations by storing and reusing the inverse matrix.
FAQs
Q: What is the inverse of a matrix?
A: The inverse of a matrix is a unique matrix that, when multiplied with the original matrix, results in the identity matrix. It allows us to efficiently solve systems of equations by storing the inverse matrix and applying it to different given vectors.
Q: Can we always find the inverse of a matrix?
A: No, the inverse of a matrix exists only for matrices that are invertible, which means their determinant is non-zero. If the determinant is zero, the matrix does not have an inverse.
Q: How does finding the inverse matrix help solve systems of equations?
A: Finding the inverse matrix allows us to solve systems of equations more efficiently. Instead of repeating the calculations for different vectors, we can store the inverse matrix and multiply it with the given vector to obtain the solution quickly.
Q: Are there other methods to solve systems of equations?
A: Yes, there are various methods to solve systems of equations, such as Gaussian elimination, Cramer’s rule, and matrix methods. Each method has its advantages and is suitable for different scenarios.
Conclusion
Solving systems of equations with multiple unknowns is a fundamental concept in mathematics. By understanding the concept of the inverse of a matrix and its practical application, we can efficiently solve different systems of equations by storing the inverse matrix. This empowers us to solve complex problems and explore various real-life scenarios where systems of equations are involved.
For more information and resources on technology and its applications, visit Techal, your go-to source for insightful analysis, informative guides, and the latest updates in the world of technology.


