When it comes to numerical integration, trapezoidal integration stands out as a more accurate method compared to the left and right rectangle approximations. In this article, we will delve into the concept of trapezoidal integration and how it can improve the accuracy of approximating integrals.
Contents
Understanding the Limitations of Rectangle Methods
In the previous part, we discussed the left and right rectangle rules, which had their own limitations. The left rectangle rule tended to underpredict the area, while the right rectangle rule tended to overpredict it. These methods failed to capture the true essence of the integral due to their simplistic assumptions.
To illustrate this, let’s consider a function, F(x), within a specific range. If we zoom in on the graph, we can observe that the left rectangle approximation fails to account for the area above the function, while the right rectangle approximation encompasses extra erroneous area. Both methods fall short in accurately representing the integral.
Introducing Trapezoidal Integration
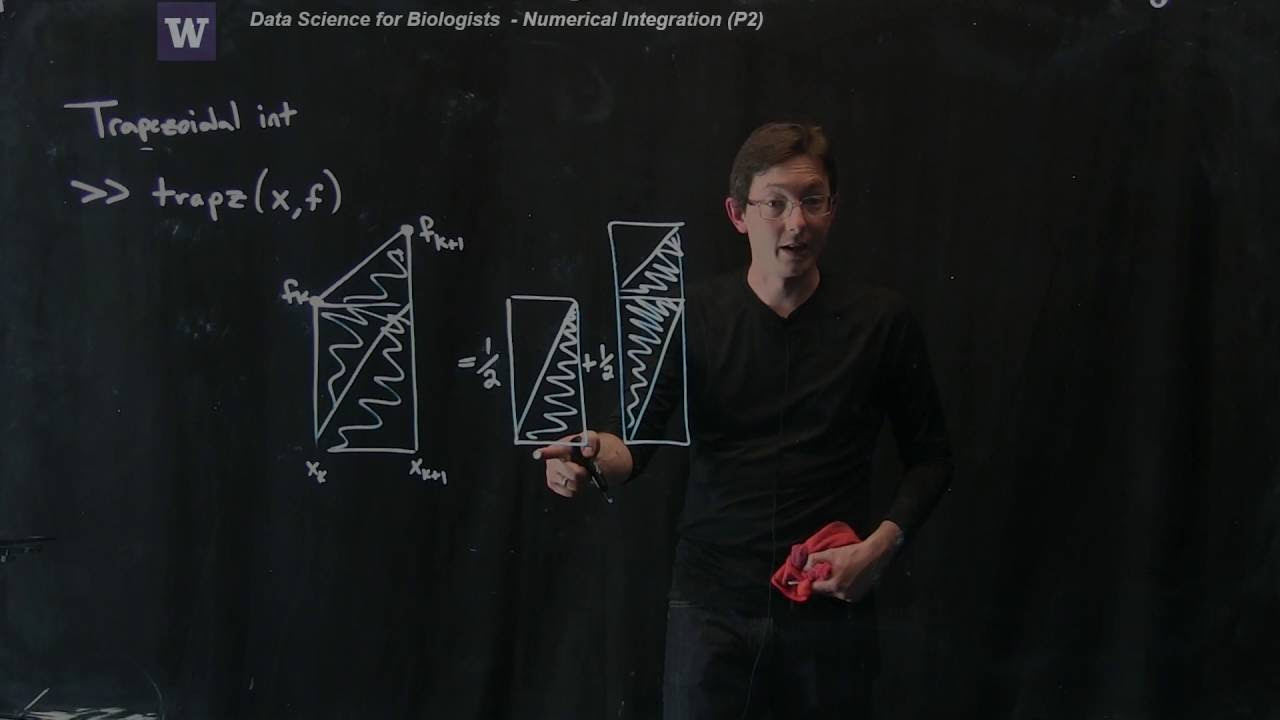
To overcome the limitations of the rectangle methods, trapezoidal integration provides a clean and effective solution. Instead of assuming the area is filled with rectangles, trapezoidal integration considers the idea of using trapezoids. By taking into account both end points, XK and XK + 1, trapezoidal integration accurately approximates the integral.
Trapezoidal integration is particularly effective when dealing with functions that have a significant positive or negative slope. It does a remarkable job of approximating the integral and outperforms the left and right rectangle methods. However, it may not be as accurate in regions where the function exhibits high curvature.
Computing Trapezoidal Integration
One of the advantages of trapezoidal integration is its ease of computation. In MATLAB, for example, you can use the built-in command trapz to calculate the area using trapezoidal integration with given X and F data points.
Alternatively, if you want to compute the area of a generic trapezoid from XK to XK + 1, you can use the simple formula:
Area = (F(XK) + F(XK + 1)) / 2 * Delta XHere, F(XK) represents the function evaluated at the left point, F(XK + 1) represents the function evaluated at the right point, and Delta X denotes the width of the interval. By summing up these trapezoid areas, you can obtain the desired result.
Comparing Numerical Methods
To showcase the effectiveness of trapezoidal integration, let’s consider an example using a sine wave. By discretizing the sine wave and applying the trapezoidal integration method, you can calculate the area accurately. This approach yields results similar to using the trapz command in MATLAB.
By coding a simple loop that iterates through the data points, you can numerically compute the trapezoidal integration. This hands-on approach provides a greater understanding of the underlying concept and empowers you to customize the integration process.
FAQs
Q: What is the advantage of trapezoidal integration over rectangle methods?
A: Trapezoidal integration improves accuracy by considering the shape of the area within the integral. It accounts for both end points and provides a more precise approximation.
Q: Can trapezoidal integration handle functions with high curvature?
A: While trapezoidal integration performs well in regions with significant slopes, it may not be as accurate in areas where the function exhibits high curvature.
Q: How can I compute trapezoidal integration in MATLAB?
A: MATLAB offers a built-in command called trapz that calculates the area using trapezoidal integration. Simply input your X and F data points, and the command will provide the desired result.
Conclusion
In this article, we explored trapezoidal integration as a more accurate alternative to rectangle methods. By considering the shape of the area within the integral, trapezoidal integration provides a better approximation. Understanding and implementing this method will enable you to achieve more accurate results in numerical integration. Visit Techal for more articles on the ever-evolving world of technology.

